疲劳裂纹扩展速率对操作条件的敏感性
简述
结构的损伤容限分析(DTA)通常是具有挑战性和耗时的努力,因为所需的数据类型和获得它所必需的技术的复杂性。所需数据的例子包括零件的应力状态如此复杂,以至于必须进行有限元分析才能获得它们。材料的疲劳裂纹扩展行为可能需要长时间的实验表征。 对时间和专业知识的高要求很容易超过现有的资源。在这种情况下,就有必要根据每条信息对最终分析的重要性来优先考虑用于获取各种信息的努力。关键因素应获得大量资源,以便准确确定。另一方面,对于次要的因素,快速近似可能是令人满意的。但问题来了,“哪些因素是关键的,哪些是次要的?”这个示例问题旨在解决这个问题。以上翻译结果来自有道神经网络翻译(YNMT)· 通用场景
数学背景:敏感性分析
在确定DTA中哪些因素重要,哪些因素不重要之前,必须选择一种方法来量化“重要”这个定性术语。在这里,我们选择使用灵敏度分析方法。它将系统输入的百分比变化与系统输出的百分比变化联系起来,两者之比就是灵敏度参数。例如,考虑下面的方程,其中x是输入,y是输出,A和n是常数。
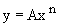
(1)
因此,y对x的灵敏度是由x的给定百分比变化引起的y的百分比变化的比率。输出y的百分比变化将表示为,对于输入变量x也是如此。

(2)
定义灵敏度参数Sy/x为百分比变化的比值,取极限为Sy/x的解析定义。
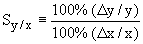
(3)
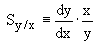
(4)
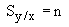
(5)
将式(4)应用于式(1)得到的结果是,无论A和x的值如何,y的变化百分比只是n乘以x的变化百分比。因此,如果n=3, x增加10%,那么y将增加30%。这是一个非常有用的结果,因为它很简单。它将在损伤容限分析的后续应用中得到广泛应用。当然,存在许多方程不是式(1)的形式。在这种情况下,式(4)必须单独应用。
损伤容限分析中的应用
应力强度因子
任何DTA最基本的步骤之一是使用式(6)计算应力强度因子K,其中b是几何因子,s是应力,a是裂纹长度。

(6)
K对各参数的敏感性说明b和s的准确值对K的计算同样重要,对裂纹长度的敏感性较小。
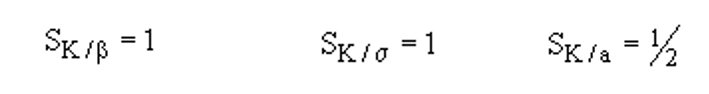
(7)
裂纹扩展速率
当分析裂纹扩展速率时,情况变得更加有趣。巴黎定律依赖于DK,假设如下,其中N是循环数,C和N是巴黎定律常数。
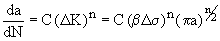
(8)
注意C和n是带有相关测量不确定度的材料特性。由于裂纹扩展速率对b因子和应力的敏感性在两种情况下都等于n,因此值得回顾典型值。图MERC-3.1显示了Al 7075-T6的裂纹扩展数据。巴黎定律在对数图上形成一条直线,n等于斜率,C等于da/dN, DK=1。可以看出,在本例中,n=3.6。(大多数材料为3£n£)该值对裂纹扩展预测的准确性具有关键影响。这意味着b因子的估计误差为10%,da/dN的预测误差为36%。同样的敏感性也适用于压力。
正是da/dN对DK的高度敏感性,反映在n值中,这对准确预测裂纹扩展速率提出了重大挑战。巴黎定律常数的敏感性呢?对C的敏感性是统一的,因为它是Eq.(8)中的指数。有必要将Eq.(4)应用到Eq.(8)中,以确定对指数n的敏感性。这样做得到,由于ln(DK)在工程分析中通常大于1,很明显,预测裂纹扩展速率对准确确定图MERC-3.1中da/ dN-DK数据斜率的敏感性甚至大于对b因子和应力的敏感性。
任务剖面数据与图MERC-2.3中的加压信息相结合,给出飞机将经历的内部加压周期的频率和幅度。 任务剖面数据由飞行高度数据与时间的关系组成。图MERC-2.4显示了一个典型的航段,由1 000英尺至25 000英尺的几个高度的任务组成。 结合图MERC-2.3和MERC-2.4中的信息,得出图MERC-2.5所示的内部加压循环。
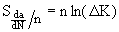
(9)
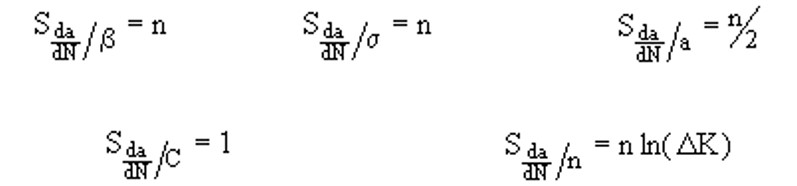
(10)
综上所述,研究结果如下
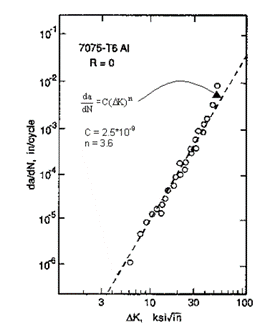
图MERC-3.1 da/dn-DK数据对7075-T6和Paris Law曲线拟合
故障使用寿命周期
DTA中主要关心的数量是组件的使用寿命,以故障周期NLife来衡量。如果忽略裂纹迟滞性,并假设b因子和应力范围在组件的整个生命周期中都是恒定的,则可以得到NLife的解析表达式。积分式(8)求解NLife,得到ao为初始裂纹长度,af为发生失效点的最终裂纹长度。
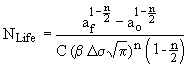
(11)
由式(11)可以看出,NLife对某些参数的敏感性仅为裂纹扩展速率对这些参数的敏感性的负数。

(12)
因此,假设n=3.6, b因子或压力增加10%将导致使用寿命减少36%。必须将式(4)应用于式(11)来确定NLife对初始裂纹长度和最终裂纹长度的敏感性。
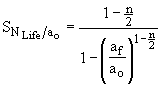
(13)
这样做就得到了公式(13)和(14)与图MERC-3.2中三个n值的ao/af的关系。
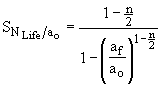
(13)
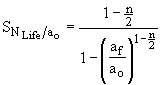
(14)
对初始裂纹长度的敏感性取决于n和af,但这些因素的公共值约为-1。因此,增加10%的初始裂纹长度导致预期疲劳寿命减少10%。另一方面,预测寿命对最终裂纹长度相对不敏感,仅显示出~10%的敏感性。因此,af增加10%只会使预期寿命增加1%。由于af通常被选为等于临界裂纹长度acrit,这表明acrit的变化对NLife估计有很小的影响。
图MECR-3.2 对于Paris公式的n的三个值,生命对初始和最终裂纹长度的感知。
假定了Paris公式、材料行为、恒定β因子和应力范围
可变b因子-数值例子
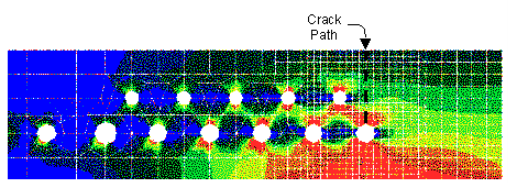
最后一个例子表明,疲劳寿命对b因子的敏感性取决于其相对值,较低的值比较大的值更关键。由于积分非常数b因子的复杂性,此分析将以数值方式而不是分析方式进行。在这个例子中,将选择飞机纵梁的水平腿。其有限元模型如图MERC-3.3所示。该部件承受张力、弯曲力和紧固件力。如图所示,裂纹从扣件孔开始,一直延伸到零件边缘。b因子如图MERC-3.4所示。
图MECR-3.3 纵梁水平支有限元模型。
裂纹起源于紧固件孔,并遵循所示路径
图MECR-3.4 图MERC-3.3中从扣件孔开始并贯穿部分的
卡板的β因子与裂纹长度的关系。
图MERC-3.4显示,由于紧固件孔处的应力集中,在较短的裂纹长度下,b因子约为3。随着裂纹长度的增加,b因子减小到约为1,当裂纹接近自由表面时,b因子再次增大。使用图MERC-3.4中的b因子的预测寿命将与其他两个进行以下修改的预测寿命进行比较。
情况1。较大的b因子值增加。B值³3增加10%,B值£1不变,中间值按比例缩放,即B值= 2增加5%。
情况2。小的b因子值增加。B值£1增加10%,B值³3不变,中间值按比例缩放,即B值= 2增加5%。
利用AFGROW预测了三种不同b因子情况下零件的疲劳寿命。其他输入包括:(1)Ds=10ksi, R=0, (2) a0=0.05 in。af=1.25英寸。(3)材料da/ dN-DK数据取自图MERC-3.1。结果如图MERC-3.5所示。
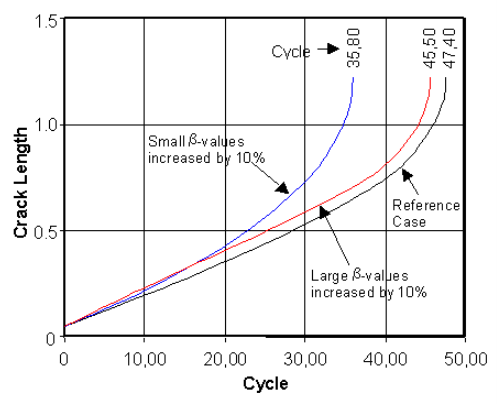
图MECR-3.5 β因子变化对预测疲劳寿命的影响。
疲劳寿命对小β值的变化比大β值的变化更敏感
小b值增加10%,预测疲劳寿命降低25%,灵敏度为-2.5。对大b值增加的敏感性为-0.4。这表明疲劳寿命对小b值的变化比大b值的变化更敏感。因此,准确确定小b因子值比确定大b因子值更重要。这是一个潜在的反直觉的结果,因为大多数分析关注大的参数值,而不是小的参数值。这种情况的存在是因为裂缝的大部分时间都在缓慢增长,长度与相应的小b因子。
总结
对影响疲劳寿命预测的因素进行了敏感性分析。研究表明,某些因素对预测寿命有很大影响,而其他因素则没有影响。重要的因素包括压力和b因素。在大多数情况下,其中任何一个增加10%都会导致预期寿命减少35%。这种高灵敏度与da/dN对DK的高灵敏度直接相关,这是一种材料性质。另一方面,对预测寿命影响相对较小的因素是临界裂纹长度和裂纹接近自由表面时出现的较大b值。
